差错控制

2022.3.9

奇偶校验码

奇偶校验码是奇校验码和偶校验码的统称,是一种最基本的检错码。它由n-1位信息元和1位校验元组成,如果是奇校验码,那么在附加一个校验元后,码长为n的码字中“1”的个数为奇数;如果是偶校验码,那么在附加一个校验元以后,码长为n的码字中“1”的个数为偶数。它只能检测奇数位的出错情况,但并不知道哪些位错了,也不能发现偶数位的出错情况。

循环冗余码（CRC）

1. 原料

   1. 帧/报文（m bit）
   2. 帧检验序列（r bit）
   3. 多项式（最高位最低位必须是1），注意从x的零次方开始！

2. 生成循环冗余码

   1. 帧除以多项式（k位），帧低位补0（k-1位）

   2. 模2除

   3. 发送待传数据+FCS（k-1位）

      

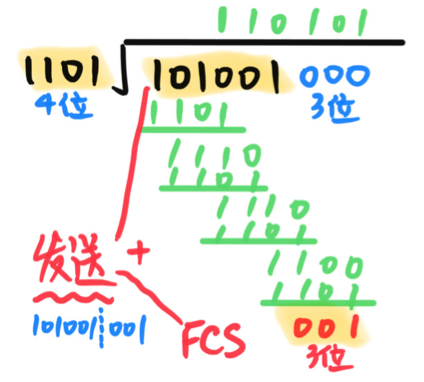
   使用举例：

   题目：要发送的数据是 1101 0110 11，采用CRC检验，生成多项式是10011（x^4+0+0+x+1），最终发送的数据是？

   方法：生成多项式10011五个数->补四个零在要发送的数据后边。摩二除生成多项式，得到的余数拼在要发送数据的后边。

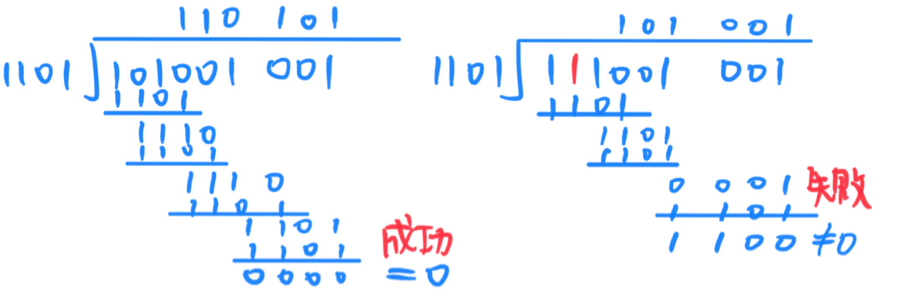
3. 接收端检验

   1. 收到的数据除以多项式，余数为0则接收

   2. n位FCS可以检测出n位错误

      

海明码

1. 码距与海明距离

   1. 码距：不同的⽐特数，⽐如001与000，码距为1。

      我的理解：

      就是码距就是不同的编码的距离，如果码距是1，就说明传错⼀位就成了别的字符的编码。如果码距是2，传错⼀位，就啥也不是，就可以判断出传错了

   2. 海明距离：对于⼀个字符集来说，所有两个编码的码距取最⼩值。

   3. 检验d位错误，码距需要d+1；纠正d位错误，码距需要2d+1。

2. 确定海明码位数(信息n位，校验k位)

   我的理解：

   校验k位可以有2^k种组合，组合种类数量需要⽐总位数n+k多，这样就可以代表哪⼀位错了

   $$\begin{array}{}\text{(1)}& n+k+1\le 2^k\end{array}$$

3. 确定校验码位置

   $$\begin{array}{}\text{(2)}& \text{信}\text{息}\text{位}& :D_4{D}_3{D}_2{D}_1\text{(3)}& \text{校}\text{验}\text{位}& :P_3{P}_2{P}_1\text{(4)}& \text{海}\text{明}\text{码}& :H_7{H}_6{H}_5{H}_4{H}_3{H}_2{H}_1\text{(5)}& \text{校}\text{验}\text{码}\text{插}\text{入}\text{位}\text{置}& :H_{2^{n-1}}=P_n\text{(6)}& \text{海}\text{明}\text{码}& :D_4{D}_3{D}_2{\mathbf{\text{P}}}_3{D}_1{\mathbf{\text{P}}}_2{\mathbf{\text{P}}}_1\end{array}$$

4. 检验关系（注意最低位是1，不是0,通常采⽤偶校验）

5. 检错纠错

不是全0，说明有错

海明码小结：

1. 检验d位错误，码距需要d+1；纠正d位错误，码距需要2d+1。
2. $n+k+1\le 2^k$$n+k+1≤2^k$，n bit数据，需要k个冗余位
3. 检验：检测位插入$2^{i-1}$$2^{i-1}$位置，（最右）代表“xx1”，偶校验
4. 纠错：偶校验成功=0。[P3,P2,P1]