数制与编码

2022.08.30

进制的转换

Overview：

1. n与十进制互转、二的倍数进制互转
2. 整数部分与小数部分

• n进制转十进制：$\sum _{i=1}^k{a}_i\cdot n^i$$\sum_{i=1}^{k}a_i\cdot n^i$

• 2、8、16进制转换：可以三个，四个二进制位为一组进行转换（小数部分也同样）

• 十进制转n进制：

  • 整数部分：辗转相除：${123}_{10}={1111011}_2$$123_{10}=1111011_2$

    我的理解：

    1. 先除出来的是经历最多2倍后剩下的，是最小的零头，所以是最低位
    2. 最后除法得0可以继续不停的除2，取余一直是0，在最高位才能不停补零

    

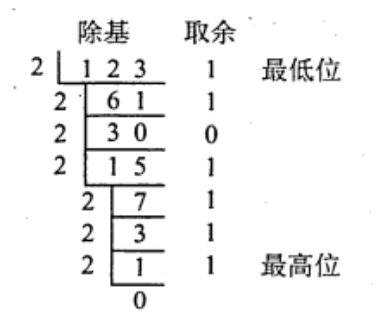
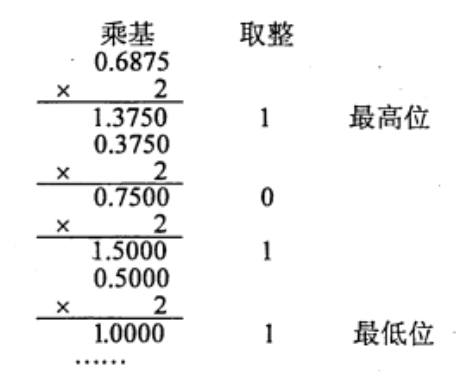
  • 小数部分：乘积取余：${0.6875}_{10}={0.1011}_2$$0.6875_{10}=0.1011_2$

    我的理解：

    一乘就取到整数了，说明它本来就很大，离小数点最近。

    

   

定点数的编码表示

1. 定点整数与小数

   1. 定点整数：符号位+数值+小数点
   2. 定点小数：符号位+小数点+数值

2. 原码

   1. 符号位：零正一负

   2. 数值：本身

   3. 表示范围关于原点对称：$[-(2^n-1),2^n-1]$$[-(2^n-1),2^n-1]$

      我的理解：因为正零和负零都是零，导致所有表示的内容正好对半分。

3. 反码

   1. 符号位：和原码一样，零正一负

   2. 数值：(负数)逐位取反

   3. 表示范围关于原点对称：$[-(2^n-1),2^n-1]$$[-(2^n-1),2^n-1]$

      我的理解：反码和原码一一对应

4. 补码

   1. 符号位：和原码一样，零正一负
   2. 数值：(负数)逐位取反(反码)+1
   3. 表示范围关于原点对称：$[-2^n,2^n-1]$$[-2^n,2^n-1]$
   4. X为负数，由$X_{\text{补}}$$X_补$求$(-X{)}_{\text{补}}$$(-X)_补$，是$X_{\text{补}}$$X_补$连同符号位一起变反，末位加一

5. 移码

6. 定点整数与小数

   n+1 bit	合法表示范围	最大的数	最小的数	真值0的表示
   整数原码	$[-(2^n-1),2^n-1]$$[-(2^n-1),2^n-1]$	$\begin{array}{rl}& 0,11\cdots 1\\ & =2^n-1\end{array}$$\begin{align}&0,11\cdots1\\&=2^n-1 \end{align}$	$\begin{array}{rl}& 1,11\cdots 1\\ & =-(2^n-1)\end{array}$$\begin{align}&1,11\cdots1\\&=-(2^n-1) \end{align}$	$\begin{array}{rl}& 0_{+}=0,000\\ & 0_{-}=1,000\end{array}$$\begin{align}&0_+=0,000\\&0_-=1,000\end{align}$
   整数反码	$[-(2^n-1),2^n-1]$$[-(2^n-1),2^n-1]$	$\begin{array}{rl}& 0,11\cdots 1\\ & =2^n-1\end{array}$$\begin{align}&0,11\cdots1\\&=2^n-1 \end{align}$	$\begin{array}{rl}& 1,00\cdots 0\\ & =-(2^n-1)\end{array}$$\begin{align}&1,00\cdots0\\&=-(2^n-1) \end{align}$	$\begin{array}{rl}& 0_{+}=0,000\\ & 0_{-}=1,111\end{array}$$\begin{align}&0_+=0,000\\&0_-=1,111\end{align}$
   整数补码	$[-2^n,2^n-1]$$[-2^n,2^n-1]$	$\begin{array}{rl}& 0,11\cdots 1\\ & =2^n-1\end{array}$$\begin{align}&0,11\cdots1\\&=2^n-1 \end{align}$	$\begin{array}{rl}& 1,00\cdots 0\\ & =-2^n\end{array}$$\begin{align}&1,00\cdots0\\&=-2^n \end{align}$	$\begin{array}{rl}& 0_{+}=0,000\end{array}$$\begin{align}&0_+=0,000\end{align}$
   小数原码	$[-(1-2^{-n}),1-2^{-n}]$$[-(1-2^{-n}),1-2^{-n}]$	$\begin{array}{rl}& 0,11\cdots 1\\ & =1-2^{-n}\end{array}$$\begin{align}&0,11\cdots1\\&=1-2^{-n}\end{align}$	$\begin{array}{rl}& 1,11\cdots 1\\ & =-(1-2^{-n})\end{array}$$\begin{align}&1,11\cdots1\\&=-(1-2^{-n}) \end{align}$	$\begin{array}{rl}& 0_{+}=0.000\\ & 0_{-}=1.000\end{array}$$\begin{align}&0_+=0.000\\&0_-=1.000\end{align}$
   小数反码	$[-(1-2^{-n}),1-2^{-n}]$$[-(1-2^{-n}),1-2^{-n}]$	$\begin{array}{rl}& 0,11\cdots 1\\ & =1-2^{-n}\end{array}$$\begin{align}&0,11\cdots1\\&=1-2^{-n}\end{align}$	$\begin{array}{rl}& 1,10\cdots 0\\ & =-(1-2^{-n})\end{array}$$\begin{align}&1,10\cdots0\\&=-(1-2^{-n}) \end{align}$	$\begin{array}{rl}& 0_{+}=0.000\\ & 0_{-}=1.111\end{array}$$\begin{align}&0_+=0.000\\&0_-=1.111\end{align}$
   小数补码	$[-1,1-2^{-n}]$$[-1,1-2^{-n}]$	$\begin{array}{rl}& 0,11\cdots 1\\ & =1-2^{-n}\end{array}$$\begin{align}&0,11\cdots1\\&=1-2^{-n}\end{align}$	$\begin{array}{rl}& 1,10\cdots 0\\ & =-1\end{array}$$\begin{align}&1,10\cdots0\\&=-1 \end{align}$	$\begin{array}{rl}& 0_{+}=0.000\end{array}$$\begin{align}&0_+=0.000\end{align}$

7. 举例

   编码	000	001	010	011	100	101	110	111
   原码	+0	+1	+2	+3	-0	-1	-2	-3
   反码	+0	+1	+2	+3	-3	-2	-1	-0
   补码	+0	+1	+2	+3	-4	-3	-2	-1
   移码	-4	-3	-2	-1	+0	+1	+2	+3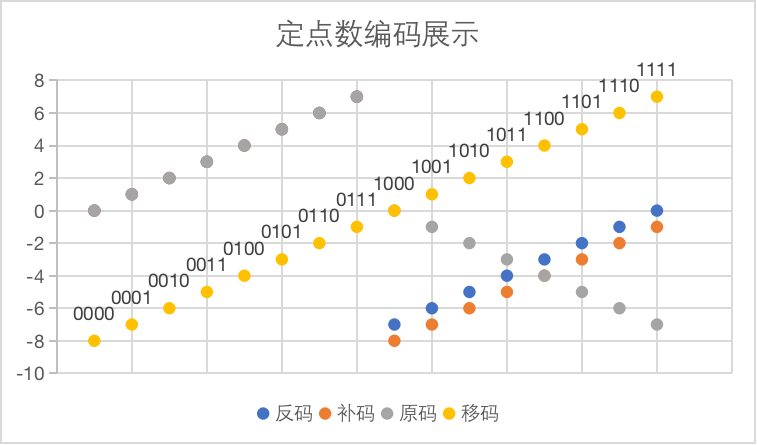

   

   我的理解：

   1. 一开始，人们为了简单的表示数字，只表示数字的绝对值

   2. 后来绝对值只能表示非负数，就在前边加一个1表示负号，诞生了【原码】

   3. 为了解决让加法与减法都只使用加法器，诞生了【反码】，比如

      $(+1)-(+2)=(+1)+(-2)={001}_{\text{反}}+{101}_{\text{反}}={110}_{\text{反}}=-1$$(+1)-(+2)=(+1)+(-2)=001_反+101_反=110_反=-1$

      $a_{\text{原}}-b_{\text{原}}=a_{\text{反}}+(-b{)}_{\text{反}}$$a_原 - b_原 = a_反 + (-b)_反$

   4. 但是反码仍然拥有两个0，我们把反码负数部分减一，就得到了【补码】，可以发现，补码仍然拥有反码的那些好处！而且还可以多表示一个数，可以理解成，原码的负零不需要了，就可以表示一个最小的数～

      $a_{\text{原}}-b_{\text{原}}=a_{\text{补}}+(-b{)}_{\text{补}}$$a_原 - b_原 = a_补 + (-b)_补$

   5. 整数补码多一个$-2^n$$-2^n$，小数补码多一个$-1$$-1$.

   6. 变形补码，就是双符号位00是正，11是负

   7. 为了比大小方便，我们把补码的符号位取反，就诞生了【移码】，这样我们就可以通过二进制大小直接确认真值的大小了了

   8. 实际上，移码的诞生是补码加一个偏执值。本例子中，偏执值是$2^3$$2^3$.

   9. 这里的偏执值是 $2^k$$2^k$ ，和但IEEE754的移码的偏执值是 $2^k-1$$2^k-1$ （普通的移码没有减1！）

8. 8421码：有权码，结果大于9，加六修正

9. 余3码：8421码结果加$(0011{)}_2$$(0011)_2$

10. 2421码：0xxx表示0-4，1xxx表示5-9

11. 例题

    1. 若$[x{]}_{\text{补}}=1,x_1{x}_2{x}_3{x}_4{x}_5{x}_6$$[x]_补=1,x_1x_2x_3x_4x_5x_6$,其中x取0或1，若要x>-32,应当满足()。

       A.x1为0，其他各位任意

       B.x1为1，其他各位任意

       C.x1为1，x2-x5中至少有一位为1

       D.x1为0，x2-x5中至少有一位为1

       【答案】：C

    2. 设x为真值，x*为其绝对值，满足$[-x\ast {]}_{\text{补}}=[-x{]}_{\text{补}}$$[-x*]_补=[-x]_补$,当且仅当()。

       A.x任意

       B.x为正数

       C.x为负数

       D.以上说法都不对

       【答案】：D

    3. 在计算机中，通常用来表示主存地址的是()。

       A,移码

       B.补码

       C.原码

       D.无符号数

       【答案】：D

    4. 关于模4补码，下列说法正的的是（）。 A. 模4 补码和模2 补码不同，它更容易检查乘除运算中的溢出问题 B. 每个模4 补码存储时只需一个符号位 C. 存储每个模4补码需要两个符号位 D. 模4补码，在算术与逻輯部件中为一个符号位

       【答案】：B. 存储模4补码需要一个符号位，ALU使用模4补码需要两个符号位

    5. 【2021 统考真题】已知带符号整数用补码表示，变量x，y，z的机器数分别为 FFFDH, FFDFH, 7FFCH，下列结论中，正确的是（ ） A. 若x,y和z为无符号整数，则z<x<y B. 若x,y和z为无符号整数，则x<y<z C. 若x,y和z为带符号整数，则x<y<z D. 若x,y和z为带符号整数，则y<x<z

       【答案】：D

       $$\begin{array}{rl}FFFDH& =1111,1111,1111,1101=1000,0000,0000,0011\\ FFDFH& =1111,1111,1101,1111=1000,0000,0010,0001\\ 7FFCH& =0111,1111,1111,1100=0111,1111,1111,1100\end{array}$$

    6. 【2015统考真题】由3个“1”和5个“0”组成的8位二进制补码，能表示的最小整数是（ ）。 【答案】：$[1,0000011{]}_{\text{补}}=[1,1111101{]}_{\text{原}}=-125$$[1,0000011]_补=[1,1111101]_原=-125$