图的遍历

2022.09.15

BFS（广度优先）

【思想】和树的层次遍历一个思想，借助一个辅助队列保存当前结点的其余的边。另外借助一个visit数组，记录哪些结点已经被访问过了。
【复杂度】

内容	时间复杂度	空间复杂度
辅助队列Q		O(V)
邻接表	O(V+E)
邻接矩阵	O(V^2)

【单源最短路径求解】也可以用visit数组保存路径长度，（之前是保存bool类型，是否访问），如果不是0代表访问过。新的结点路径长度为刚才结点路径+1即可。
【广度优先生成树，生成森林】

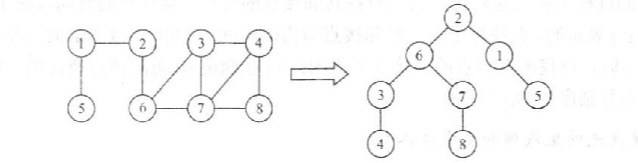
DFS（深度优先）

【思想】类似于树的先序遍历，借助递归/栈实现。
【复杂度】

内容	时间复杂度	空间复杂度
递归形成的栈		O(V)
邻接表	O(V+E)
邻接矩阵	O(V^2)

【深度优先生成树，生成森林】

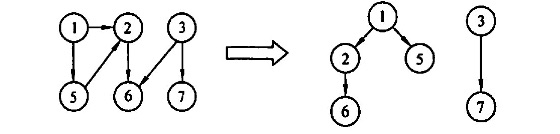
例题

下列关于广度优先算法的说法中，正确的是（）
I. 当各边的权值相等时，广度优先算法可以解决单源最短路径问题 II. 当各边的权值不等时，广度优先算法可用来解决单源最短路径问题 III.广度优先遍历算法类似于树中的后序遍历算法 IV. 实现图的广度优先算法时，使用的数据结构是队列 A. I、 IV B. II、III、IV C. II、IV D. I、III、IV
【答案】：A
对于一个非连通无向图G，采用深度优先遍历访问所有顶点，在 DFSTraverse 函数(见考点讲解DFS 部分）中调用DFS 的次数正好等于（）。 A.顶点数 B.边数 C.连通分量数 D.不确定
【答案】：A -> C
对一个有n个顶点、e条边的图来用邻接表表示时，进行DFS 遍历的时问复杂度为(），空间复杂度为（)：进行BFS 遍历的时问复杂度为（），空间复杂度为（）. A. O(n) B. O(e) C. O(n+e) D. O(1)
【答案】：CACA
对有n个顶点、e条边的图采用邻接短阵表示时，进行 DFS 遍历的时问复杂度为（），进行 BFS 遍历的时间复杂度为（） A. O(n^2) B. O(e) C. O(n+e) D. O(e^2)
【答案】：AA
无向图G=(V,E)，其中 V={a,b,c,d,e,f}，E={(a,b),(a,e), (a,c), (b,e),(c,f),(f,d),(e,d)}，对该图从a开始进行深度优先遍历，得到的顶点序列正确的是(）. A. a, b, e, c, d,f B. a, c,f, e, b, d C. a, e, b, c,f, d D. a, e, d, f, c, b
【答案】：abedcf,acfd,aed，D
如下图所示，在下面的5个序列中，符合深度优先遍历的序列个数是(）。
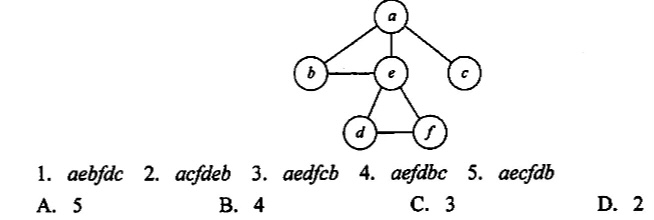
【答案】：D
用邻接表存储的图的深度优先遍历算法类似于树的（），而其广度优先遍历算法类似于树的（）。 A. 中序遍历 B. 先序遍历 C. 后序遍历 D. 按层次遍历
【答案】：BD
一个有向图G的邻接表存储如下图所示，从项点1出发，对图G调用深度优先遍历所得项点序列是（ )；按广度优先遍历所得项点序列是（）
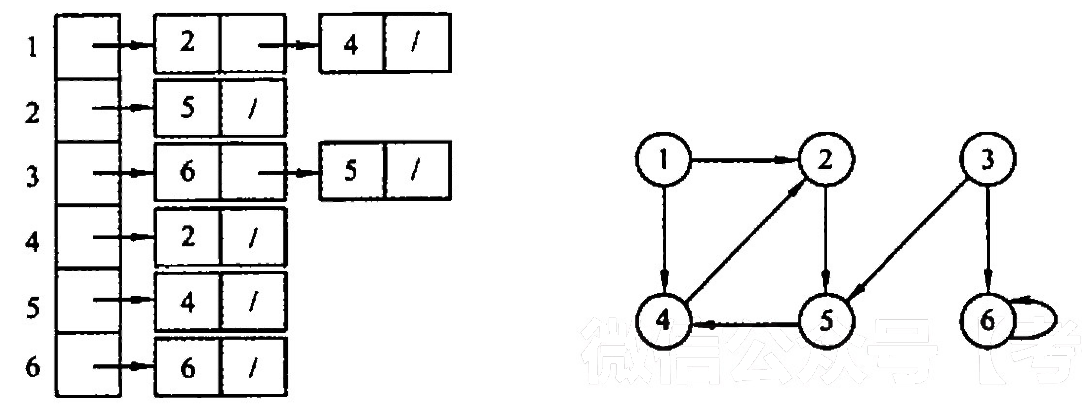
A. 125436 B. 124536 C. 124563 D. 362514
【答案】：A、B
无向图G=(V，E），其中V={a.b,c,d.e.f}，E={(a, b),(a.e),(a,c),(b,e),(c,f),(f,d),(e,d)}，对图进行深度优先遍历，不能得到的序列（）
A. acfdeb B. aebdfc C. aedfcb D. abecdf
【答案】：acfdeb，aebdfc，aedfcb，D
判断有向图中是否存在回路，除可以利用拓扑排序外，还可以利用（）。 A. 求关键路径的方法 B.求最短路径的 Dikstra 算法 C.深度优先遍历算法 D.广度优先遍历算法
【答案】：C
使用DFS 算法递归地遍历一个无环有向图，并在退出递归时输出相应顶点，这样得到的顶点序列是（）。 A. 逆拓扑有序 B. 拓扑有序 C. 无序的 D. 都不是
【答案】：A
设无向图G=(V，E），和G'=(V',E')，若G'是G的生成树，则下列说法中错误的是( )。 A. G'为G的子图 B. G'为G的连通分量 C. G'为G的极小连通子图且V=M D. G'是G的一个无环子图
【答案】：B
图的广度优先生成树的树高比深度优先生成树的树高（）。 A. 小或相等 B. 小 C. 大或相等 D. 大
【答案】：A
对有n个顶点、e条边且使用邻接表存储的有向图进行广度优先遍历，其算法的时问复杂度是（）。 A. O(n) B. O(e) C. O(n+e) D. O(ne)
【答案】：C
【2013 统考真题】若对如下无向图进行遍历，則下列选项中，不是广度优先遍历序列的是（）
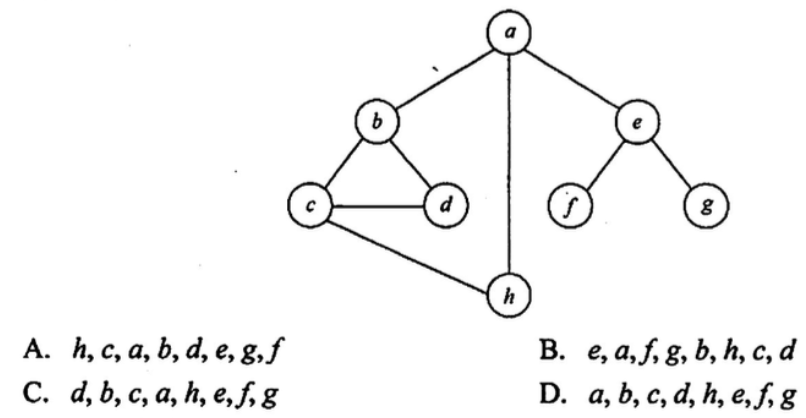
【答案】：hcabde，eafgb[hcd]，dbca[he]，a[bhe] D
【2015 统考真题】设有向图G-(V，E)的，顶点集V= （V0，V1,V2，V3)，边集B={(V0,V1),(V0,V2),(V0,V3),(V1,V3)}。若从顶点V0开始对图进行深度优先遍历，則可能得到的不同遍历序列个数是（）。 A. 2 B.3 C. 4 D.5
【答案】：D
. 【2016 统考真题】下列选项中，不是下图深度优先搜索序列的是
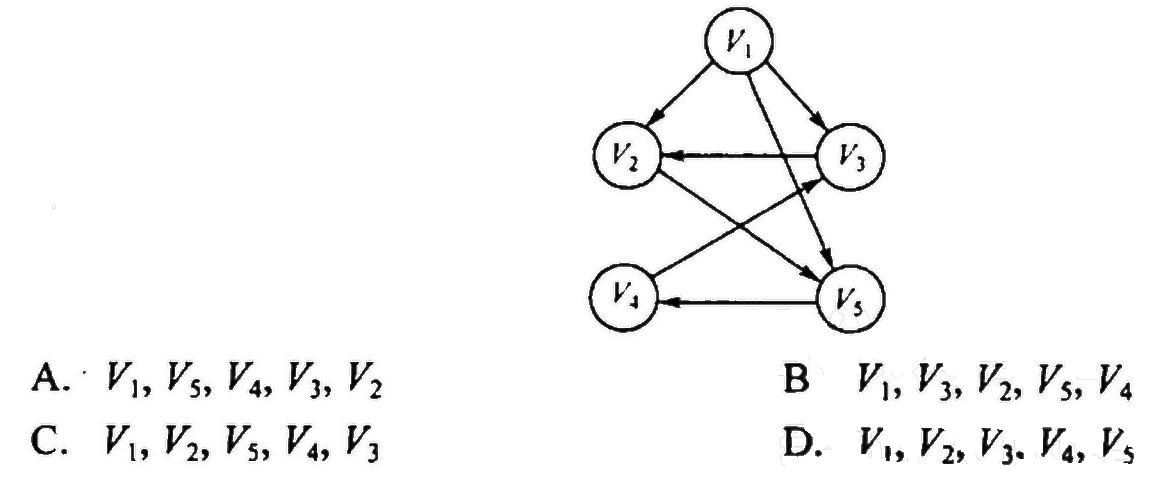
【答案】：D

源码


#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
//#include "AdjacencyMatrix.h" // 邻接矩阵
//typedef MGraph Graph; 不能正常运行，可能因为先import的邻接矩阵
//#include "AdjacencyList.h" // 邻接表
typedef LGraph Graph;

void visit(int v){
  printf("%d ",v);
}

// 广度优先遍历辅助数组
bool BFSvisited[MaxVerNum]={0};

// 广度优先遍历(顶点)
void BFS(Graph G, int v, bool init=true){
  /** 初始化广度优先遍历辅助数组
   * 1. 如果需要初始化则将所有位置为未访问
   * 2. 不需要初始化的情况:BFS遍历森林
   */
  if(init)
    for(int i=1;i<GetVexnum(G)+1;i++)
      BFSvisited[i]=false;
  /** 广度优先遍历辅助队列 
   * 1. 开启BFS访问结点(首结点
   * 2. 依次访问结点(队列出队) , 结点的子节点如果未访问就入队
   */
  LinkQueue Q;
  LinkQueueInit(Q);
  visit(v);
  BFSvisited[v]=true;
  LinkQueueEn(Q, ele_build(v));
  Element e;
  while(!LinkQueueEmpty(Q)){
        LinkQueueDe(Q,e);
        v = ele_get_weight(e);
    for(int w=FirstNeighbor(G,v);w>=0;w=NextNeighbor(G,v,w)){
      if(!BFSvisited[w]){
        visit(w);
        BFSvisited[w]=true;
                LinkQueueEn(Q, ele_build(w));
      }
    }
  }
}

// 广度优先遍历(图)
void BFSTraverse(Graph G){
  for(int i=1;i<GetVexnum(G)+1;i++)
      BFSvisited[i]=false;
  for(int i=1;i<GetVexnum(G)+1;i++)
    if(!BFSvisited[i])
      BFS(G,i,false);
}

// 深度优先遍历辅助队列
bool DFSvisited[MaxVerNum] = {false};

// 深度优先遍历(点)
void DFS(Graph G, int v, bool init=true){
  if(init)
    for(int i=1;i<GetVexnum(G)+1;i++)
      DFSvisited[i]=false;
  visit(v);
  DFSvisited[v]=true;
  for(int w=FirstNeighbor(G,v);w>=0;w=NextNeighbor(G,v,w))
    if(!DFSvisited[w])
      DFS(G,w,false); 
}

// 深度优先遍历(图)
void DFSTraverse(Graph G){
  for(int i=1;i<GetVexnum(G)+1;i++)
      DFSvisited[i]=false;
  for(int i=1;i<GetVexnum(G)+1;i++)
    if(!DFSvisited[i])
      DFS(G,i,false);
}

void test_graph_traverse()
{
  printf("图的遍历\n");
  Graph G;
  TestInit(G);

  printf("\n广度优先遍历(2):");
  BFS(G,2);
  printf("\n广度优先遍历(5):");
  BFS(G,5);
  printf("\n广度优先遍历(7):");
  BFS(G,7);
  printf("\n广度优先遍历(图):");
  BFSTraverse(G);

  printf("\n深度优先遍历(2):");
  DFS(G,2);
  printf("\n深度优先遍历(图):");
  DFSTraverse(G);
}

输出结果


图的遍历
 1 -> 2( 1) 
 2 -> 6( 1) 1( 1) 
 3 -> 4( 1) 7( 1) 6( 1) 
 4 -> 8( 1) 7( 1) 3( 1) 
 5 
 6 -> 7( 1) 3( 1) 2( 1) 
 7 -> 8( 1) 4( 1) 3( 1) 6( 1) 
 8 -> 7( 1) 4( 1) 

 1 - 2   3 - 4
     | / | / |
 5   6 - 7 - 8

广度优先遍历(2):2 6 1 7 3 8 4 
广度优先遍历(5):5 
广度优先遍历(7):7 8 4 3 6 2 1 
广度优先遍历(图):1 2 6 7 3 8 4 5 
深度优先遍历(2):2 6 7 8 4 3 1 
深度优先遍历(图):1 2 6 7 8 4 3 5