二叉树的概念

2022.12.10

基本概念

• 满二叉树与完全二叉树

  

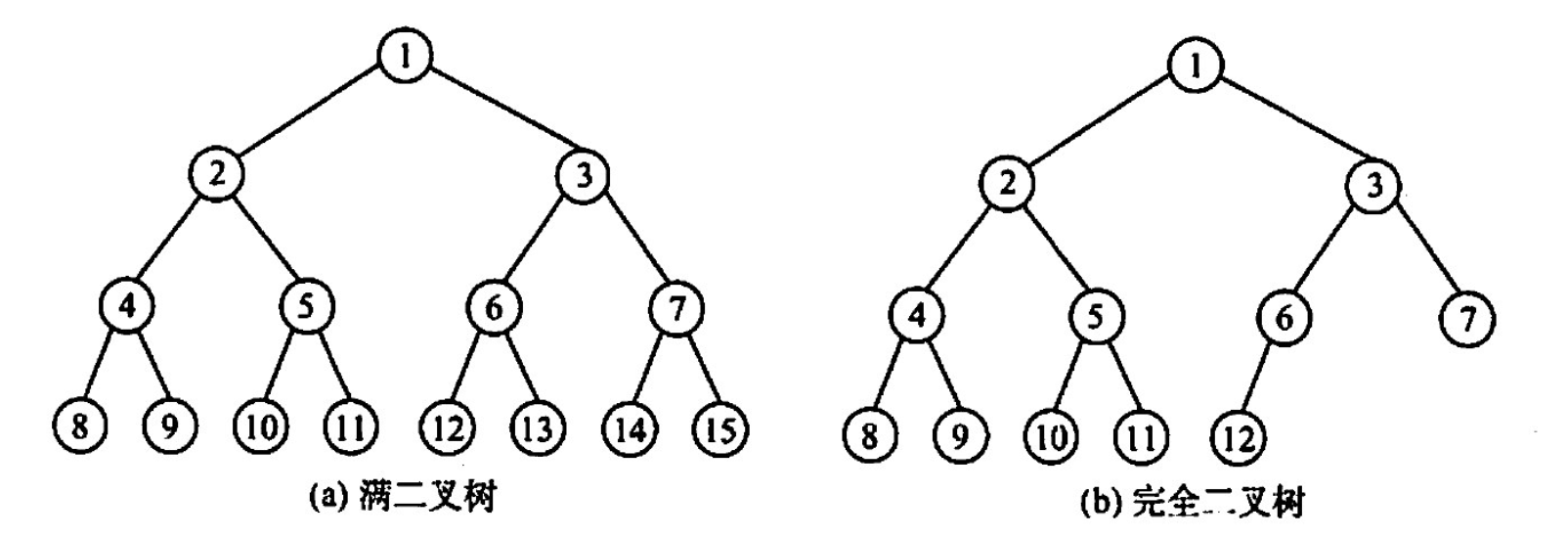
  • 分支结点：$i\le \lfloor \frac{n}{2}\rfloor$$i≤\lfloor \frac{n}{2} \rfloor$

• 二叉排序树

• 平衡二叉树：左右子树深度不超过一

• 二叉树的性质：

  • 非空二叉树叶子结点树n0 = 度为2的结点数n2 + 1

    $$\begin{array}{}\text{(2)}& n_0=n_2+1\end{array}$$

  • 非空二叉树第k层上最多有2^k个结点

  • i的左孩子为2i

  • i的右孩子为2i+1

  • 结点i的深度 = $\lfloor {\log }_{2}i\rfloor +1$$\lfloor \log_2i \rfloor+1$

• 二叉树的顺序存储

  • i的左孩子是2i
  • i的右孩子是2i+1
  • 不是二叉树不能用顺序存储

• 二叉树的链式存储

  • n个结点的二叉链表有n+1个空链域 「n+1 = 2n-(n-1)」

例题

1. 下列关于二叉树的说法中，正确的是（ ） A. 度为2的有序树就是二叉树 B. 含有n个结点的二叉树的高度为$\lfloor {\log }_{2}n\rfloor +1$$\lfloor \log_2n \rfloor+1$ C. 在完全二叉树中，若一个结点没有左孩子，则它必是叶结点 D. 在任意一棵非空二叉排序树中，删除某结点后又将其插入，则所得二叉排序树与删除前原二叉排序树相同

   【答案】：C

2. 以下说法中，正确的是（ ）。 A. 在完全二叉树中，叶子结点的双亲的左兄弟（若存在）一定不是叶子结点 B. 任何一棵二叉树，叶子结点个数为度为2的结点数减1，即n0=n2-1 C. 完全二叉树不适合顺序存储结构，只有满二叉树适合顺序存储结构 D. 结点按完全二叉树层序编号的二叉树中，第i个结点的左孩子的编号为2i

   【答案】：A

3. 具有10个叶子结点的二叉树中有（ ）个度为2的结点。 A. 8 B. 9 C. 10 D. 11

   【答案】：B

4. 设高度为h的二叉树上只有度为0和度为2的结点，则此类二叉树中所包含的结点数至少为（ ） A. h B. 2h - 1 C. 2h+1 D. h+1

   【答案】：B

5. 假设一棵二叉树的结点个数为 50，则它的最小高度是( )。 A. 4 B. 5 C. 6 D. 7

   【答案】：C

6. 设二叉树有2n个结点，且m＜n，则不可能存在（ ）的结点。 A. n个度为0 B. 2m个度为0 C. 2m个度为1 D. 2m个度为2

   【答案】：D -> C

7. 一个具有1025个结点的二叉树的高h为（）。 A. 11 B. 10 C. 11~ 1025 D. 10~1024

   【答案】：C

8. 设二叉树只有度为0和2的结点，其结点个数为 15，则该二叉树的最大深度为( )。 A. 4 B. 5 C. 8 D. 9

   【答案】：C

9. 高度为h的完全二叉树最少有（ ）个结点。 A. 2^h B 2^h+1 C 2^{h-1} D. 2^h-1

   【答案】：C

10. 已知一棵完全二叉树的第6层（设根为第1层）有8个叶结点，则完全二叉树的结点个数最少是（）。 A.39 B. 52 C. 111 D. 119

    【答案】：A

11. 若一棵深度为6的完全二叉树的第6层有3个叶子结点，则该二叉树共有（ ）个叶子结点 A. 17 B. 18 C. 19 D 20

    【答案】：A

12. 一颗完全二叉树上有1001个结点，其中叶结点的个数是（ ） A. 250 B. 500 C. 254 D. 501

    【答案】：D

13. 若一颗二叉树有126个结点，在第7层（根结点在第1层）至多有（ ）个结点。 A. 32 B. 64 C. 63 D. 不存在第7层

    【答案】：C

14. 一棵有 124 个叶子结点的完全二又树，最多有（ ）个结点。 A. 247 B. 248 C. 249 D. 250

    【答案】：A -> B，因为加一个左孩子，叶子结点个数不变！

15. 一棵有n个结点的二叉树来用二叉链存储结点，其中空指针为（ ） A. n B. n+1 C. n-1 D. 2n

    【答案】：B

16. 在一棵完全二叉树中，其根的序号为1，（ ）可判定序号为p和q的两个结点是否在同一层。 A. $\lfloor {\log }_{2}p\rfloor$$\lfloor \log_2p \rfloor$ = $\lfloor {\log }_{2}q\rfloor$$\lfloor \log_2q \rfloor$ B. ${\log }_{2}p$$\log_2p$ = ${\log }_{2}q$$\log_2q$ C. $\lfloor {\log }_{2}p\rfloor +1$$\lfloor \log_2p\rfloor+1$ = $\lfloor {\log }_{2}q\rfloor$$\lfloor \log_2q \rfloor$ D. $\lfloor {\log }_{2}p\rfloor$$\lfloor \log_2p\rfloor$ = $\lfloor {\log }_{2}q\rfloor +1$$\lfloor \log_2q \rfloor+1$

    【答案】：A

17. 假定一棵三叉树的结点数为50，則它的最小高度为（ ）。 A. 3 B. 4 C. 5 D. 6

    【答案】：C

18. 已知一採有2011 个结点的树，其叶结点个数是116，该树对应的二叉树中无右孩子的结点个数是（ ）。 A. 115 B. 116 C. 1895 D. 1896

    【答案】：D

19. 对于一棵满二叉树，共有n个结点和m个叶子结点，高度为h，则（ ）。 A. n=h+m B.n+m=2h C.m=h-1 D. n=2^h -1

    【答案】：D

20. 【2009 统考真题】已知一棵完全二叉树的第6层（设根为第1层）有8个叶结点，则该完全二叉树的结点个数最多是(） A. 39 B. 52 C. 111 D. 119

    【答案】：A -> C。第六层可以全满，然后通过接第七层，让第六层只剩8个叶子结点！

21. 【2011 統考真题】若一棵完全二叉树有768个结点，则该二叉树中叶结点的个数是(）. A. 257 B. 258 C. 384 D. 385

    【答案】：C

22. 【2018 统考真题】设一棵非空完全二叉树T的所有叶结点均位于同一层，且每个非叶结点都有2个子结点。若T有k个叶结点，则T的结点总数是（ ）。 A. 2k-1 B. 2k C. k^2 D. 2^k - 1

    【答案】：A

23. 【2020 统考真题】对于任意一棵高度为 5且有10个结点的二叉树，若来用顺序存储结构保存，每个结点占 1个存储单元（仅存放结点的数据信息），则存放该二叉树需要的存储单元数量至少是（）. A. 31 B. 16 C. 15 D. 10

    【答案】：A