无穷级数
2022.06.29
常数项级数
概念与性质
正项级数
收敛原则
比较判别法
比较判别法的极限形式
比值判别法(达朗贝尔判别法)
收敛发散失效 根值判别法(柯西判别法)
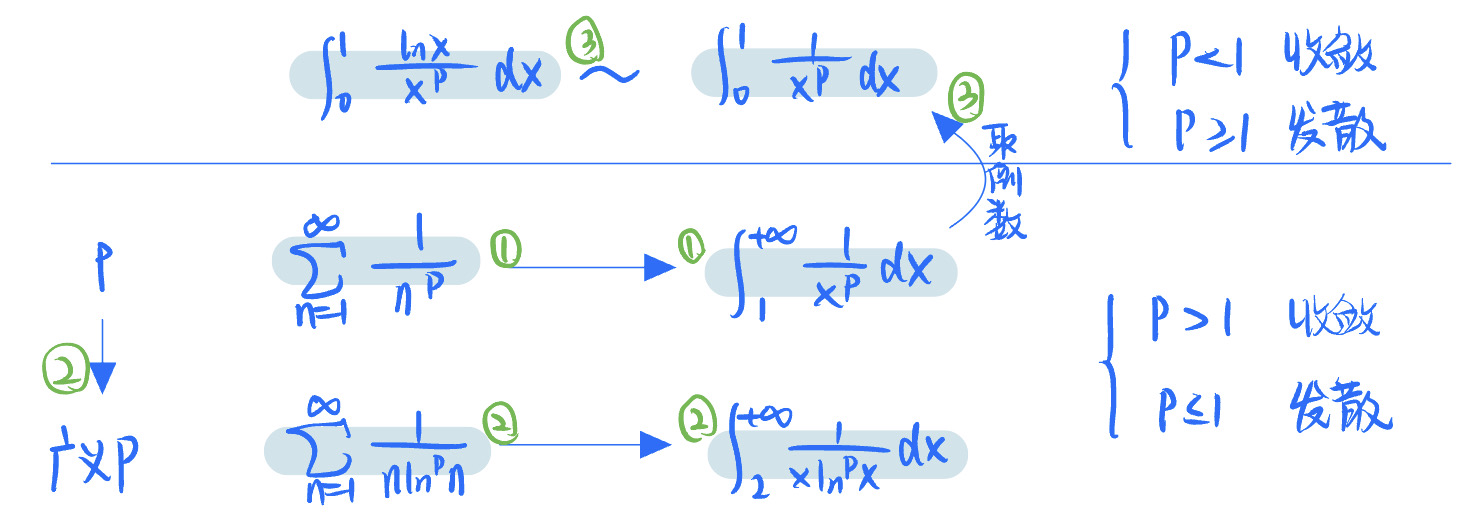
收敛发散失效 积分判别法
非负单减,与同敛散
交错级数
任意项级数
绝对收敛与条件收敛
- 绝对收敛:同项加绝对值也收敛,绝对收敛则原级数也收敛
- 条件收敛:原级数收敛但是加绝对值就不收敛了
常用结论
收敛收敛收敛,发散 收敛收敛不确定为任意项收敛,发散 收敛收敛不确定为任意项收敛,发散 收敛收敛收敛,发散 收敛收敛收敛,发散 收敛与收敛不确定为任意项收敛,发散 收敛收敛收敛则收敛错!还需要发散 收敛不确定收敛,发散 收敛收敛收敛收敛发散 收敛则收敛发散则收敛 收敛则绝对收敛因为 则在中只有有两个收敛,另一个必收敛 都收敛,则收敛 收敛发散,则发散 都发散,则发散都发散,则不确定任意 都收敛,收敛收敛任意不确定不确定
幂级数
幂级数与收敛域
函数项级数
幂级数
阿贝尔定理
注意端点要单独确认 收敛域求法(具体型)
收敛区间为范围注意端点要单独确认,得到收敛域 抽象型,对于
若时条件收敛到的变换不改变收敛域包括乘与平移对级数逐项求导,收敛半径不变,收敛域可能缩小对级数逐项积分,收敛半径不变,收敛域可能扩大 如何改造通项与下标
先导后积
先积后导
常用结论
常用的展开式(注意收敛域)
函数展开
常用的求和公式
